
von Günther Rosenbaum
Yspahan ist ein Spiel von Sebastian Pauchon, das im Oktober 2006 im Ystari-Verlag erschienen ist.
Eine Rezension dieses Spieles ist auf unserer Homepage an anderer Stelle zu finden - hier möchte ich mich nur mit dem sehr originellen und innovativen Würfelmechanismus beschäftigen und die Wahrscheinlichkeiten für das Auftreten verschiedener interessanter Würfelkonstellationen berechnen.
 |
| Es ist klar, dass auf der zweitobersten Zeile mit der "Vase" nur selten Würfel liegen werden! |
Standardmäßig würfelt man mit 9 Würfeln - man kann aber gegen Abgabe von Gold bis zu 3 weitere Würfel kaufen.
Der Würfelwurf wird nun sortiert: Alle 1er zusammen, alle 2er, ..., alle 6er. Dann werden diese Würfelgruppen auf das rechts abgebildete Tableau abgelegt:
Ein Beispiel von so einem Würfelergebnis sieht man im Bild rechts: Man erkennt hier, dass unterhalb der Zeile "Gold" Lücken entstehen können.
und
Bei der Planung der eigenen Spielstrategie muss man diese Ereignisse in etwa abschätzen können - daher werde ich die berechneten Wahrscheinlichkeiten hier aufführen. Bei der Planung muss man natürlich berücksichtigen, welche "Gebäudeeigenschaften" man zusätzlich nutzen kann, und dass man gegen Abgabe einer "Karte" die Größe einer Würfelgruppe künstlich um 1 erhöhen kann.
| 9 W6 | min 1 | min 2 |
| Gold | 100 | 59 |
Dies ist eine Tabelle für den Wurf mit 9 sechsseitigen Würfeln (9 W6); alle Zahlenwerte sind auf ganzzahlige Prozentwerte gerundete Wahrscheinlichkeiten.
Da die Gruppe mit der höchsten Zahl IMMER auf das "Gold" gelegt wird (außer in dem unwahrscheinlichen Fall eines Wurfes von lauter gleichen Zahlen), ist hier die Wahrscheilichkeit 100%, dass mindestens 1 Würfel dort liegt.
Mindestens 2 Würfel (also 2,3, 4, ...oder 9) auf dem Goldfeld findet man noch mit einer Wahrscheinlichkeit von 59%.
Achtung:
Wenn in den Tabellen der Wert 100% auftaucht, so ist dies immer ein gerundeter Wert und in
Wirklichkeit irgendetwas zwischen ca. 99,5% und 100%! Aber solche kleinen Unterschiede sind für die
Strategiediskussionen völlig uninteressant - daher werden hier alle Wahrscheinlichkeiten immer auf
ganze Prozent gerundet.
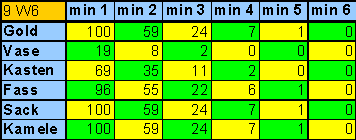 |
| Tabelle 1
Wahrscheinlichkeiten für den Wurf mit 9 sechsseitigen Würfeln! |
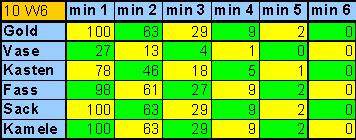 |
| Tabelle 2
Wahrscheinlichkeiten für den Wurf mit 10 sechsseitigen Würfeln! |
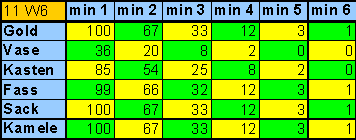 |
| Tabelle 3
Wahrscheinlichkeiten für den Wurf mit 11 sechsseitigen Würfeln! |
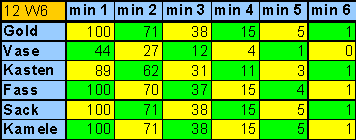 |
| Tabelle 4
Wahrscheinlichkeiten für den Wurf mit 12 sechsseitigen Würfeln! |
Am Anfang des Spieles oder wenn man die "Karawanenstrategie" verfolgt, braucht man womöglich nur "Masse" - egal auf welchem der 6 Felder viele Würfel liegen, Hauptsache es sind viele!
Daher die folgende Tabelle 5:
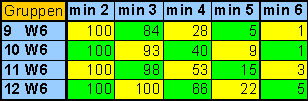 |
| Tabelle 5
Wahrscheinlichkeit für den Wurf von großen Gruppen! |
Aus den obigen Tabellen mag nun jeder seine eigenen Schlussfolgerungen ziehen und seine Strategien entsprechend anpassen. Auf einige Beobachtungen möchte ich aber trotzdem hinweisen:
Bei fester Würfelanzahl unterscheiden sich die Wahrscheinlichkeiten in den Zeilen für Gold, Kamele, Sack und Fass nur geringfügig ! Als Daumenwert erreicht man dort in etwa mit der Wahrscheinlichkeit 1, 2/3, 1/3 eine Gruppe von mindestens 1, 2 oder 3 Würfeln.
Interessant sind daher die "Kasten-" und "Vasenfelder".
Hier stelle ich noch mal in einer gesonderten Tabelle gegenüber, wie sich die Wahrscheinlichkeiten verändern, wenn man zu den 9 Standardwürfeln zusätzliche hinzu kauft:
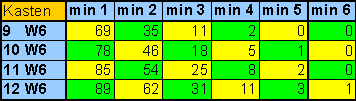 |
| Tabelle 6
Wahrscheinlichkeit für Würfelgruppen auf dem "Kastenfeld" bei steigender Anzahl von Würfeln! |
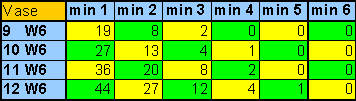 |
| Tabelle 7
Wahrscheinlichkeit für Würfelgruppen auf dem "Vasenfeld" bei steigender Anzahl von Würfeln! |
Bei diesen beiden Feldern verändert der Zukauf von Würfeln schon einiges an den Wahrscheinlichkeiten ! (Daumenwert: knapp 10% pro Würfel bei den "min 1" Werten)
Der Siegpunktwert auf dem Spielplan ist in etwa:
Mit 2 Steinen im "Kastenfeld" erhält man 4 Siegpunkte - genauso viele, wie mit 1 Stein im "Vasenfeld". Die Wahrscheinlichkeit, mindestens 2 Würfel im "Kastenfeld" zu erreichen ist aber durchweg größer, als mindestens 1 Würfel im "Vasenfeld" zu bekommen. Also werden wohl langfristig im Mittel Steine im "Kastenfeld" etwas ertragreicher sein als die Steine im Vasenfeld !
Viel Spaß noch bei diesem wirklich schönen Spiel.
| Kommentare anschauen/schreiben |
©2006, Westpark Gamers